(e) Descriptive Statistics
Physical Geographers often collect quantitative information about natural phenomena to further knowledge in their field of interest. This collected data is then often analyzed statistically to provide the researcher with impartial and enlightening presentation, summary, and interpretation of the phenomena understudy. The most common statistical analysis performed on data involves the determination of descriptive characteristics like measures of central tendency and dispersion.
It usually is difficult to obtain measurements of all the data available in a particular system of interest. For example, it may be important to determine the average atmospheric pressure found in the center of hurricanes. However, to make a definitive conclusion about a hurricane's central pressure with 100% confidence would require the measuring of all the hurricanes that ever existed on this planet. This type of measurement is called a population parameter. Under normal situations, the determination of population parameters is impossible, and we settle with a subset measure of the population commonly called an estimator. Estimators are determined by taking a representative sample of the population being studied.
Samples are normally taken at random. Random sampling implies that each measurement in the population has an equal chance of being selected as part of the sample. It also ensures that the occurrence of one measurement in a sample in no way influences the selection of another. Sampling methods are biased if the recording of some influences the recording of others or if some members of the population are more likely to be recorded than others.
Measures of Dispersion
Measures of central tendency provide no clue into how the observations are dispersed within the data set. Dispersion can be calculated by a variety of descriptive statistics including the range, variance, and standard deviation. The simpest measure of dispersion is the range.
Table 3e-2: Dates of the first fall frost at Somewhere, USA, for an 11-year period.
The range for the data is set is derived by subtracting 279 (the smallest value) from 314 (the largest value). The range is 35 days.
The first step in the calculation of standard deviation is to determine the variance by obtaining the deviations of the individual values (Xi) from the mean (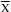 ). The formula for variance (S2) is:
). The formula for variance (S2) is:
S2 = [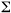 (Xi -
(Xi -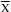 )2] /(N-1)
)2] /(N-1)
where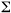 is the summation sign, (Xi -
is the summation sign, (Xi - 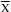 )2 is calculated (third column), and N is the number of observations. Standard deviation (S) is merely the square root of the variance (
)2 is calculated (third column), and N is the number of observations. Standard deviation (S) is merely the square root of the variance (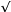 S2 ).
S2 ).
In the case of the Somewhere data, the standard deviation is:
S2 = 1356 / 10
S = 11.6 or 12 (to the nearest day)
CITATION
Physical Geographers often collect quantitative information about natural phenomena to further knowledge in their field of interest. This collected data is then often analyzed statistically to provide the researcher with impartial and enlightening presentation, summary, and interpretation of the phenomena understudy. The most common statistical analysis performed on data involves the determination of descriptive characteristics like measures of central tendency and dispersion.
It usually is difficult to obtain measurements of all the data available in a particular system of interest. For example, it may be important to determine the average atmospheric pressure found in the center of hurricanes. However, to make a definitive conclusion about a hurricane's central pressure with 100% confidence would require the measuring of all the hurricanes that ever existed on this planet. This type of measurement is called a population parameter. Under normal situations, the determination of population parameters is impossible, and we settle with a subset measure of the population commonly called an estimator. Estimators are determined by taking a representative sample of the population being studied.
Samples are normally taken at random. Random sampling implies that each measurement in the population has an equal chance of being selected as part of the sample. It also ensures that the occurrence of one measurement in a sample in no way influences the selection of another. Sampling methods are biased if the recording of some influences the recording of others or if some members of the population are more likely to be recorded than others.
Measures of Central Tendency
Collecting data to describe some phenomena of nature usually produces large arrays of numbers. Sometimes it is very useful to summarize these large arrays with a single parameter. Researchers often require a summary value that determines the center in a data sample's distribution. In orther words, a measure of the central tendency of the data set. The most common of these measures are the mean, the median, and the mode.
Table 3e-1 describes a 15-year series of number of days with precipitation in December for two fictitious locations. The following discussion describes the calculation of the mean, median, and mode for this sample data set.
Table 3e-1 describes a 15-year series of number of days with precipitation in December for two fictitious locations. The following discussion describes the calculation of the mean, median, and mode for this sample data set.
Table 3e-1: Number of days with precipitation in December for Piney and Steinback, 1967-81.
| Year | Piney | Steinback |
| 1967 | 10 | 12 |
| 1968 | 12 | 12 |
| 1969 | 9 | 13 |
| 1970 | 7 | 15 |
| 1971 | 10 | 13 |
| 1972 | 11 | 9 |
| 1973 | 9 | 16 |
| 1974 | 10 | 11 |
| 1975 | 9 | 12 |
1976
|
13
|
13
|
1977
|
8
|
10
|
1978
|
9
|
9
|
1979
|
10
|
13
|
1980
|
8
|
14
|
1981
|
9
|
15
|
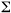 (Xi) (Xi) |
144
|
187
|
| N | 15 | 15 |
The mean values of these two sets is determined by summing of the yearly values divided by the number of observations in each data set. In mathematical notation this calculation would be expressed as:
mean (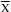 ) = S(Xi)/N
) = S(Xi)/N
where Xi is the individual values,
N is the number of values, and
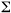 is sigma, a sign used to show summation.
is sigma, a sign used to show summation.
Thus, the calculate means for Piney and Steinback are:
mean (
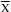 ) = S(Xi)/N
) = S(Xi)/N where Xi is the individual values,
N is the number of values, and
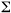 is sigma, a sign used to show summation.
is sigma, a sign used to show summation. Thus, the calculate means for Piney and Steinback are:
Piney mean = 10 (rounded off)
Steinback mean = 13 (rounded off)
The mode of a data series is that value that occurs with greatest frequency. For Piney, the most frequent value is 9 which occurs five times. The mode for Steinback is 13.
The third measure of central tendency is called the median. The median is the middle value (or the average of the two middle values in an even series) of the data set when the observations are organized in ascending order. For the two locations in question, the medians are:
Piney
9, 9, 10, 11, 12, 12, 12, 13, 13, 13, 13, 14, 15, 15, 16
median = 13
Steinback
7, 8, 8, 9, 9, 9, 9, 9, 10, 10, 10, 10, 11, 12, 13
median = 9
Steinback mean = 13 (rounded off)
The mode of a data series is that value that occurs with greatest frequency. For Piney, the most frequent value is 9 which occurs five times. The mode for Steinback is 13.
The third measure of central tendency is called the median. The median is the middle value (or the average of the two middle values in an even series) of the data set when the observations are organized in ascending order. For the two locations in question, the medians are:
Piney
9, 9, 10, 11, 12, 12, 12, 13, 13, 13, 13, 14, 15, 15, 16
median = 13
Steinback
7, 8, 8, 9, 9, 9, 9, 9, 10, 10, 10, 10, 11, 12, 13
median = 9
Measures of Dispersion
Measures of central tendency provide no clue into how the observations are dispersed within the data set. Dispersion can be calculated by a variety of descriptive statistics including the range, variance, and standard deviation. The simpest measure of dispersion is the range.
The range is calculated by subtracting the smallest individual value from the largest. When presented together with the mean, this statistic provides a measure of data set variability. The range, however, does not provide any understanding to how the data are distributed about the mean. For this measurement, the standard deviation is of value.
The following information describes the calculation of the range, variance, and standard deviation for the data set in Table 3e-2.
The following information describes the calculation of the range, variance, and standard deviation for the data set in Table 3e-2.
Table 3e-2: Dates of the first fall frost at Somewhere, USA, for an 11-year period.
| Day of First Frost * (Xi) |
Xi -
|
(Xi -
|
| 291 |
-8
|
64
|
| 299 |
0
|
0
|
| 279 |
-20
|
400
|
| 302 |
3
|
9
|
| 280 |
-19
|
361
|
| 303 |
4
|
16
|
| 299 |
0
|
0
|
| 304 |
5
|
25
|
| 307 |
8
|
64
|
| 314 |
15
|
225
|
| 313 |
14
|
196
|
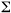 (Xi)
= 3291 (Xi)
= 3291 |
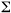 (Xi
- (Xi
- |
|
| *The dates are given in year days, i.e., January 1st is day 1, January 2nd is day 2, and so on throughout the year. |
The range for the data is set is derived by subtracting 279 (the smallest value) from 314 (the largest value). The range is 35 days.
The first step in the calculation of standard deviation is to determine the variance by obtaining the deviations of the individual values (Xi) from the mean (
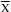 ). The formula for variance (S2) is:
). The formula for variance (S2) is: S2 = [
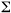 (Xi -
(Xi -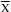 )2] /(N-1)
)2] /(N-1) where
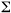 is the summation sign, (Xi -
is the summation sign, (Xi - 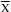 )2 is calculated (third column), and N is the number of observations. Standard deviation (S) is merely the square root of the variance (
)2 is calculated (third column), and N is the number of observations. Standard deviation (S) is merely the square root of the variance (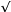 S2 ).
S2 ). In the case of the Somewhere data, the standard deviation is:
S2 = 1356 / 10
S = 11.6 or 12 (to the nearest day)
This value provides significant information about the distribution of data around the mean. For example:
(a) The mean ± one sample standard deviation contains approximately 68% of the measurements in the data series.
(b) The mean ± two sample standard deviations contains approximately 95% of the measurements in the data series.
In Somewhere, the corresponding dates for fall frosts ± one and two standard deviations from the mean (day 299) are:
Minus two standard deviations: 299 - 24 = 275
Minus one standard deviation: 299 - 12 = 287
Plus one standard deviation: 299 + 12 = 311
Plus two standard deviations: 299 + 24 = 323
The calculations above suggest that the chance of frost damage is only 2.5% on October 2nd (day 275), 16% on October 15th (day 287), 50% on October 27th (day 299), 84% on November 8th (day 311), and 97.5% on November 20th (day 323).
(b) The mean ± two sample standard deviations contains approximately 95% of the measurements in the data series.
In Somewhere, the corresponding dates for fall frosts ± one and two standard deviations from the mean (day 299) are:
Minus two standard deviations: 299 - 24 = 275
Minus one standard deviation: 299 - 12 = 287
Plus one standard deviation: 299 + 12 = 311
Plus two standard deviations: 299 + 24 = 323
The calculations above suggest that the chance of frost damage is only 2.5% on October 2nd (day 275), 16% on October 15th (day 287), 50% on October 27th (day 299), 84% on November 8th (day 311), and 97.5% on November 20th (day 323).
CITATION
Pidwirny, M. (2006). "Descriptive Statistics". Fundamentals of Physical Geography, 2nd Edition. 29/12/2011. http://www.physicalgeography.net/fundamentals/3e.html
Do you like this post? Please link back to this article by copying one of the codes below.
URL: HTML link code: BB (forum) link code: