(g) Inferential Statistics: Comparison of Sample Means
U = n1•n2 + {n1•(n1 + 1)}/2 - S r1
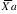= 9.08
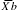= 10.77
na = 25 nb = 26
To test the hypothesis that there is no difference between strawberry varieties we compute:
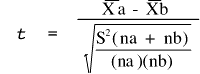
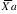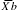where : and are the arithmetic means for groups A and B, na and nb are the number of observations in groups A and B, and S2 is the pooled within-group variance.
To compute the pooled within variance, we calculate the corrected sum of squares (SS) within each treatment group.
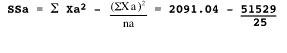
= 2091.04 - 2061.16 = 29.88
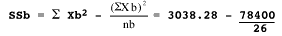
= 3038.28 - 3015.38 = 22.90
Then the pooled variance is
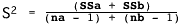
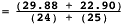
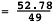
= 1.077
and,
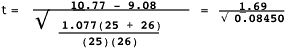
= 5.814
In this case, the critical t value with 49 degrees of freedom at the 0.01 probability level is approximately 2.682. Since our sample is greater than this, the difference is significant at the 0.01 level and we can reject the null hypothesis.
The Paired t-Test
The previous description for the t-test assumed that the random samples are drawn from the two populations independently. However, there are some situations where the observations are paired. Analyzing paired data is done differently than if the two samples are independent. This modified procedure is known as a paired t-test. Most statistical software programs that perform the Student's t-test have options to select for either a paired or unpaired analysis.
CITATION
U = n1•n2 + {n1•(n1 + 1)}/2 - S r1
U = 13 • 15 + {13•(13 + 1)}/2 - 267 = 19
U1 = n1•n2 + {n2•(n2 + 1)}/2 - S r2
U1 = 13 • 15 + {15•(15 + 1)}/2 - 139 = 176
where n1 is the number of observations in the first sample, and n2 is the number of observations in the second sample.
The lower of these two values (U and U1) is then taken to determine the significance of the difference between the two data sets. Calculated from the data found on Table 3g-1, the value of U is 19 and U1 is 176. The lower value is thus 19. This value is now compared to the critical value found on the significance tables for the Mann-Whitney U (Table 3g-2) at a pre-determined significance level for the given sample sizes. An important feature of this statistical test is that the greater the difference between the two sets of samples, the smaller will be the test statistic (i.e., the lower value of U or U1). Thus, if the computed value is lower than the critical value in Table 3g-2, the null hypothesis (H0) is rejected for the given significance level. If the computed value is greater than the critical value, we then accept the null hypothesis.
Using a significance level of 0.05 with sample sizes of n1 = 13 and n2 = 15, the critical value in the table for a two-tailed test is 54. Note that this is a two-tailed test, because the direction of the relationship is not specified. The computed value of U is 19, which is much less than the tabulated value. Thus, the null hypothesis (H0) is rejected and the alternative hypothesis (H1) is accepted.
U1 = 13 • 15 + {15•(15 + 1)}/2 - 139 = 176
where n1 is the number of observations in the first sample, and n2 is the number of observations in the second sample.
The lower of these two values (U and U1) is then taken to determine the significance of the difference between the two data sets. Calculated from the data found on Table 3g-1, the value of U is 19 and U1 is 176. The lower value is thus 19. This value is now compared to the critical value found on the significance tables for the Mann-Whitney U (Table 3g-2) at a pre-determined significance level for the given sample sizes. An important feature of this statistical test is that the greater the difference between the two sets of samples, the smaller will be the test statistic (i.e., the lower value of U or U1). Thus, if the computed value is lower than the critical value in Table 3g-2, the null hypothesis (H0) is rejected for the given significance level. If the computed value is greater than the critical value, we then accept the null hypothesis.
Using a significance level of 0.05 with sample sizes of n1 = 13 and n2 = 15, the critical value in the table for a two-tailed test is 54. Note that this is a two-tailed test, because the direction of the relationship is not specified. The computed value of U is 19, which is much less than the tabulated value. Thus, the null hypothesis (H0) is rejected and the alternative hypothesis (H1) is accepted.
Table 3g-2: Critical values of U for the Mann-Whitney U test (P = 0.05).
n
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
1
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
2
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
0
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
1
|
2
|
2
|
2
|
2
|
3
|
-
|
-
|
-
|
-
|
0
|
1
|
1
|
2
|
2
|
3
|
3
|
4
|
4
|
5
|
5
|
6
|
6
|
7
|
7
|
8
|
4
|
-
|
-
|
-
|
-
|
-
|
-
|
3
|
4
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
11
|
12
|
13
|
13
|
5
|
-
|
0
|
1
|
2
|
2
|
3
|
5
|
6
|
7
|
8
|
9
|
10
|
12
|
13
|
14
|
15
|
17
|
18
|
19
|
20
|
6
|
-
|
-
|
-
|
-
|
-
|
5
|
6
|
8
|
10
|
11
|
13
|
14
|
16
|
17
|
19
|
21
|
22
|
24
|
25
|
27
|
7
|
-
|
-
|
-
|
-
|
-
|
-
|
8
|
10
|
12
|
14
|
16
|
18
|
20
|
22
|
24
|
26
|
28
|
30
|
32
|
34
|
8
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
13
|
15
|
17
|
19
|
22
|
24
|
26
|
29
|
31
|
34
|
36
|
38
|
41
|
9
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
17
|
20
|
23
|
26
|
28
|
31
|
34
|
37
|
39
|
42
|
45
|
48
|
10
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
23
|
26
|
29
|
33
|
36
|
39
|
42
|
45
|
48
|
52
|
55
|
11
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
30
|
33
|
37
|
40
|
44
|
47
|
51
|
55
|
58
|
62
|
12
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
37
|
41
|
45
|
49
|
53
|
57
|
61
|
65
|
69
|
13
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
45
|
50
|
54
|
59
|
63
|
67
|
72
|
76
|
14
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
55
|
59
|
64
|
67
|
74
|
78
|
83
|
15
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
64
|
70
|
75
|
80
|
85
|
90
|
16
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
75
|
81
|
86
|
92
|
98
|
17
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
87
|
93
|
99
|
105
|
18
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
99
|
106
|
112
|
19
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
113
|
119
|
20
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
127
|
Another statistical test used to determine differences between two samples of the same phenomenon is the Student's t-test. The Student's t-test, however, differs from the Mann-Whitney U test in that it is used with data that is normally distributed (parametric).
Table 3g-3 describes the data from two "treatments" of strawberry plants that were subjected to freezing temperatures over an equal period of days. The data displayed are the numbers of fruit produced per plant. The treatments consist of genetically engineered and control (normal) varieties.
H0 : there is no difference in the number of strawberries produced by the control and genetically engineered varieties.
H1 : there is a difference in the number of strawberries produced by the control and genetically engineered varieties.
Table 3g-3 describes the data from two "treatments" of strawberry plants that were subjected to freezing temperatures over an equal period of days. The data displayed are the numbers of fruit produced per plant. The treatments consist of genetically engineered and control (normal) varieties.
H0 : there is no difference in the number of strawberries produced by the control and genetically engineered varieties.
H1 : there is a difference in the number of strawberries produced by the control and genetically engineered varieties.
Table
3g-3: Strawberry
data.
Control
(Xa)
|
(Xa)2
|
Engineered
(Xb)
|
(Xb)2
|
10.7
|
114.49
|
10.0
|
100
|
6.7
|
44.89
|
10.2
|
104.04
|
8.7
|
75.69
|
12.0
|
144
|
8.3
|
68.89
|
10.5
|
110.25
|
10.6
|
112.36
|
10.3
|
106.09
|
8.3
|
68.89
|
9.4
|
88.36
|
10.0
|
100
|
9.7
|
94.09
|
9.8
|
96.04
|
12.7
|
161.29
|
9.1
|
82.81
|
10.4
|
108.16
|
9.8
|
96.04
|
10.8
|
116.64
|
8.9
|
79.21
|
12.3
|
151.29
|
10.3
|
106.09
|
11.0
|
121
|
8.3
|
68.89
|
12.3
|
151.29
|
9.4
|
88.36
|
10.8
|
116.64
|
8.8
|
77.44
|
10.6
|
112.36
|
10.9
|
118.81
|
10.1
|
102.01
|
9.4
|
88.36
|
10.7
|
114.49
|
7.9
|
62.41
|
10.2
|
104.04
|
8.3
|
68.89
|
9.5
|
90.25
|
8.6
|
73.96
|
11.0
|
121
|
11.1
|
123.21
|
9.4
|
88.36
|
8.8
|
77.44
|
10.2
|
104.04
|
7.5
|
56.25
|
11.2
|
125.44
|
8.9
|
79.21
|
10.5
|
110.25
|
7.9
|
62.41
|
11.9
|
141.61
|
-
|
-
|
12.3
|
151.29
|
|
S Xa =
227
|
S Xa2 = 2091.04 | S Xb = 280 | S Xb2 = 3038.28 |
(S Xa)2 =
51,529
|
(S Xb)2 = 78,400 |
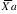= 9.08 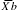= 10.77 na = 25 nb = 26
To test the hypothesis that there is no difference between strawberry varieties we compute:
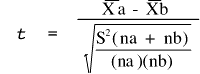
where :
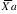and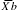 are the arithmetic means for groups A and B, na and nb are the number of observations in groups A and B, and S2 is the pooled within-group variance. To compute the pooled within variance, we calculate the corrected sum of squares (SS) within each treatment group.
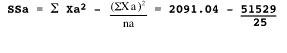
= 2091.04 - 2061.16 = 29.88
= 3038.28 - 3015.38 = 22.90
Then the pooled variance is
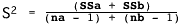
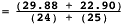
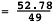
= 1.077
and,
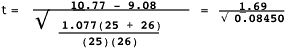
= 5.814
This value of t has (na - 1) + (nb - 1) degrees of freedom. If it exceeds the tabular value of t (Table 3g-4) at a pre-determined probability level, we can reject the null hypothesis, and the difference between the two means would be considered statistically significant (greater than would be expected by chance if there is actually no difference).
In this case, the critical t value with 49 degrees of freedom at the 0.01 probability level is approximately 2.682. Since our sample is greater than this, the difference is significant at the 0.01 level and we can reject the null hypothesis.
The Paired t-Test
The previous description for the t-test assumed that the random samples are drawn from the two populations independently. However, there are some situations where the observations are paired. Analyzing paired data is done differently than if the two samples are independent. This modified procedure is known as a paired t-test. Most statistical software programs that perform the Student's t-test have options to select for either a paired or unpaired analysis.
Table 3g-4: Critical values of Student's t-distribution (2-tailed).
| Degrees
of Freedom |
P=0.10 | P=0.05 | P=0.02 | P=0.01 | P=0.001 | Degrees
of Freedom |
| 1 | 6.314 | 12.706 | 31.821 | 63.657 | 636.619 | 1 |
| 2 | 2.920 | 4.303 | 6.965 | 9.925 | 31.598 | 2 |
| 3 | 2.353 | 3.182 | 4.541 | 5.841 | 12.924 | 3 |
| 4 | 2.132 | 2.776 | 3.747 | 4.604 | 8.610 | 4 |
| 5 | 2.015 | 2.571 | 3.365 | 4.032 | 6.869 | 5 |
| 6 | 1.943 | 2.447 | 3.143 | 3.707 | 5.959 | 6 |
| 7 | 1.895 | 2.365 | 2.998 | 3.499 | 5.408 | 7 |
| 8 | 1.860 | 2.306 | 2.896 | 3.355 | 5.041 | 8 |
| 9 | 1.833 | 2.262 | 2.821 | 3.250 | 4.781 | 9 |
| 10 | 1.812 | 2.228 | 2.764 | 3.169 | 4.587 | 10 |
| 11 | 1.796 | 2.201 | 2.718 | 3.106 | 4.437 | 11 |
| 12 | 1.782 | 2.179 | 2.681 | 3.055 | 4.318 | 12 |
| 13 | 1.771 | 2.160 | 2.650 | 3.012 | 4.221 | 13 |
| 14 | 1.761 | 2.145 | 2.624 | 2.977 | 4.140 | 14 |
| 15 | 1.753 | 2.131 | 2.602 | 2.947 | 4.073 | 15 |
| 16 | 1.746 | 2.120 | 2.583 | 2.921 | 4.015 | 16 |
| 17 | 1.740 | 2.110 | 2.567 | 2.898 | 3.965 | 17 |
| 18 | 1.734 | 2.101 | 2.552 | 2.878 | 3.922 | 18 |
| 19 | 1.729 | 2.093 | 2.539 | 2.861 | 3.883 | 19 |
| 20 | 1.725 | 2.086 | 2.528 | 2.845 | 3.850 | 20 |
| 21 | 1.721 | 2.080 | 2.518 | 2.831 | 3.819 | 21 |
| 22 | 1.717 | 2.074 | 2.508 | 2.819 | 3.792 | 22 |
| 23 | 1.714 | 2.069 | 2.500 | 2.807 | 3.767 | 23 |
| 24 | 1.711 | 2.064 | 2.492 | 2.797 | 3.745 | 24 |
| 25 | 1.708 | 2.060 | 2.485 | 2.787 | 3.725 | 25 |
| 26 | 1.706 | 2.056 | 2.479 | 2.779 | 3.707 | 26 |
| 27 | 1.703 | 2.052 | 2.473 | 2.771 | 3.690 | 27 |
| 28 | 1.701 | 2.048 | 2.467 | 2.763 | 3.674 | 28 |
| 29 | 1.699 | 2.045 | 2.462 | 2.756 | 3.659 | 29 |
| 30 | 1.697 | 2.042 | 2.457 | 2.750 | 3.646 | 30 |
| 40 | 1.684 | 2.021 | 2.423 | 2.704 | 3.551 | 40 |
| 60 | 1.671 | 2.000 | 2.390 | 2.660 | 3.460 | 60 |
| 120 | 1.658 | 1.980 | 2.358 | 2.617 | 3.373 | 120 |
CITATION
Pidwirny, M. (2006). "Inferential Statistics: Comparison of Sample Means". Fundamentals of Physical Geography, 2nd Edition. 29/11/2011. http://www.physicalgeography.net/fundamentals/3g.html